April 2020, Vol. 247, No. 4
Features
Buried Pipe Failures Dependent on Soil Stiffness, Too
By Agostino Napolitano, Pipeline Department Manager, and Angelina Parlato, Onshore Pipeline Techical Manager, Saipem SpA
Performance limits and potential failures must be identified for buried pipe design. Chief among those are excessive deformations of the pipe, wall buckling and collapse.
Maximum allowable pipe deflection is usually not determined by structural failure but by conditions such as clearance for pipe-cleaning equipment, special sections and pipe appurtenances (attachments). Pipeline designers classify pipes as “flexible” or “rigid,” depending on how they perform after installation.
Flexible pipe can move, or deflect, under loads without structural damage, while rigid pipes cannot deflect significantly without structural distress, such as cracking. From the standpoint of rigidity, pipes were classified by Marston in 1930:
Rigid conduits: The cross-sectional shapes cannot be distorted sufficiently to change the vertical or horizontal dimensions more than 0.1% without causing materially injurious cracks.
Semirigid conduits: The cross-sectional shapes can be distorted sufficiently to change the vertical or horizontal dimensions more than 0.1%, but not more than 3% without causing materially injurious cracks.
Flexible conduits: The cross-sectional shapes can be distorted sufficiently to change the vertical or horizontal dimensions more than 3% before causing materially injurious cracks.
In reality, the behavior of a buried pipeline will depend on how its stiffness compares with the stiffness of the soil in which it is buried. The soil-pipe system is statically indeterminate. As such, the interface pressure between the soil and pipe cannot be calculated by static responses alone.
As soil and surface loads are placed over a buried pipe, the ring tends to deflect primarily into an ellipse with a decrease in the vertical diameter and an almost equal (slightly less) increase in horizontal diameter. The increase in horizontal diameter develops lateral soil support that increases the load-carrying capacity of the pipe. The decrease in vertical diameter partially relieves the ring of load since the soil above the pipe takes more of the load in an arching action over the pipe.
Soil-Pipe System
The amount of deflection induced by installation that will occur in any buried pipe depends on three factors: pipe stiffness, soil stiffness and earth load and surface load due to construction equipment.
Measurements made by Marston and Spangler equations reveal the load on a flexible pipe is substantially less than that on a rigid pipe. The level of lateral earth load also depends on the nature of the backfill and its level of compaction, as well as the stiffness of the side walls of a trench, if the pipe sits in a trench rather than in an embankment fill.
Therefore, it should be readily apprγeciated that the backfill and its construction are vital to the performance of a flexible pipe. Unfortunately, designers have placed too much attention on the structural properties of the pipe rather than on the soil.
There are many pertinent variables in the complex interaction of pipe and soil. For pipes, one widely recognized variable is pipe flexibility, D/t, which is an inverse form of pipe stiffness, EI/D3, and may be used for analyses involving pipe stiffness of plain steel pipe (no mortar linings or coatings).
Pipe flexibility, D/t, normally ranges between 30 and 100 for oil and gas onshore pipelines. Another common variable is pipe deflection, x/D. For soil, the most pertinent variables are the friction angle, ϕ, and the vertical strain of sidefill embedment, ε. An approximation of strain is given by ε = σ/E’, where σ is the vertical soil stress and E’ is the soil stiffness modulus.
Soil modulus is not a modulus of elasticity nor a constant. It is often found, approximately, as the slope of a secant to the stress-strain diagram from laboratory compression tests. The confined compression test is conservative since the laboratory sample is subject to a confining pressure and compressed vertically.
Sidefill soil, on the opposite, is compressed vertically, compressed horizontally (radially) and confined longitudinally (biaxial compression) for which the compression (vertical strain) is less than it is for confined compression tests. To define if the behavior of a pipe is flexible or rigid, it is convenient to consider the stiffness ratio, Rs, as the ratio between soil stiffness and pipe stiffness:
Rs = E’ / (EI/D3) = E’D3/EI [Eq. 1-1]
Where:
E’ is the soil stiffness modulus of the soil (slope of a secant on the stress strain diagram); and
EI/D3 = E/12(D/t)3 is the pipe stiffness, where I is the transverse moment of inertia per unit length of individual pipe wall components.
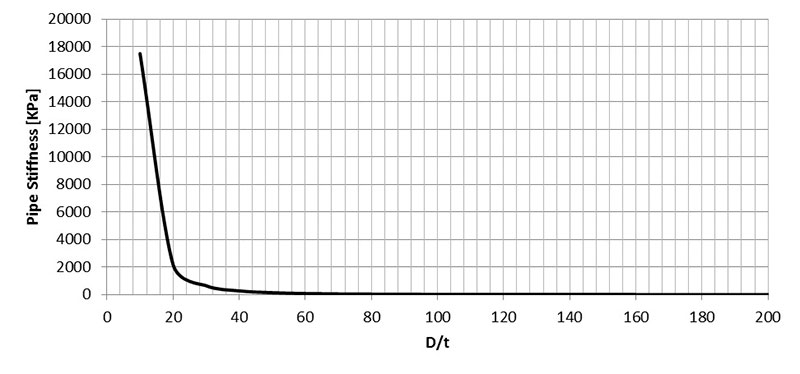
Soil stiffness, E’, can vary from 100 kPa for damped soil to 50-100 MPa for well-compacted, coarse-grained soil. Pipe stiffness, EI/D3, is inversely related to pipe flexibility, D/t, and reduces progressively to zero for high D/t values. Usually pipe stiffness contributes significant resistance to pipe deflection if Rs is less than about 200, or D/t is less than 50 (Figure 2). Conversely, soil stiffness is crucial for flexible pipes and Rs is usually greater than 200.
Pipe Deflection
To predict pipe deflection of buried circular pipes, designers normally use the modified IOWA formula. The formula is given by the ratio between the load acting on the pipe and the soil-pipe stiffness according to Equation [1-2]:
Where, in SI units:
Δx = Horizontal deflection [m]
DL = Deflection lag factor
K = Bedding constant
W = Earth load on pipe = γHD [kN/m]
r = Mean pipe radius [m]
E = Modulus of tensile elasticity of the pipe material [kPa]
I = Moment of inertia per unit length [m3]
E’ = Modulus of soil reaction [kPa]
Under most soil conditions, flexible pipe tends to deflect into a nearly elliptical shape and the horizontal and vertical deflections may be considered equal for small deflections (Δ).
The relationship between horizontal deflection and vertical deflection in buried flexible conduit was determined in the laboratory for pipe of various sizes at deflections under 10% by Spangler in the following equation:
Δx = 0.913 Δy
where:
Δx = Horizontal deflection
Δy = Vertical deflection
The deflection lag factor (DL) accounts for the fact that, in soil-pipe systems, the soil consolidation at the sides of the pipe continues at an ever-decreasing rate with time, after the maximum load reaches the buried pipe. Experience demonstrates that deflection of buried flexible pipe will continue for a period of time after completion of pipe installation before final equilibrium is achieved.
Spangler originally said, “The deflection lag factors observed in the experiments range from 1.38 to 1.46, and in no instance was equilibrium completely attained.”
His experience had shown deflections could increase by as much as 30% over 40 years. For this reason, he recommended the incorporation of a deflection lag factor of 1.5 as a conservative design procedure.
It should be noted, however, that the load proposed by Spangler in the formula is the Marston load for a flexible pipe, which is smaller than the prism load (often 1.5 times smaller). For a pipe with good flexibility, the long-term load will not exceed the prism load. The increase in load with time is the largest contribution to increasing deflection. Therefore, for design, the prism load can be used to compensate for the increased trench consolidation load with time and resulting increased deflection. When deflection calculations are based on prism loads, the DL should be 1.0.
The bedding constant K accommodates the response of the buried pipe to the opposite and equal reaction to the load force derived from the bedding under the pipe. The bedding constant varies with the width and angle of the bedding achieved in the installation. Table 1, published in 1941, provides values determined, theoretically, by Spangler.
Bedding Angle (Degrees) K
0 0.110
30 0.108
45 0.105
60 0.102
90 0.096
120 0.090
180 0.083
Table 1: Bedding constants
The modulus of soil reaction E’ is not the same as defined in Equation [1-1]. Many research efforts have been attempted to measure E’, without much success. The most useful method has involved the measurement of deflections of a buried pipe for which installation conditions are known, followed by a back calculation through the IOWA formula to determine the real value of E’.
Hartley and Duncan, in 1987, gave a range of E’, varying with soil types, compaction levels and cover depths. Their work also suggested to assume E’ equal to the soil-constrained modulus, which can be based on laboratory tests. Jeyapalan and Watkins have recalculated the values of E’, published by Howard (1977), finding that E’ can vary several hundred percent from the one predicted, and showing how difficult it is to predict that value.
Maximum through-wall circumferential bending stress due to ovalization can be determined from Equation [1-2] as:

This stress equation is used in the American Society of Civil Engineers American Lifelines Alliance (ASCE ALA) guidelines to account for the stresses due to ovalization on a buried pipelines. Pipe deflections and pipe through-wall bending stress, therefore, are related.
Figure 3 shows how pipe deflections and through-wall bending stress (assuming a steel pipe with E = 2.1E + 8KPa, X60, soil density γ = 20KN/m3, DL = 1; K = 0,1) ranges as a function of D/t and E’. It can be noted that pipes with low pipe flexibility, D/t, do not require soil compaction since deformation limits are not likely to be reached for standard cover depths. On the opposite, higher D/t implies the need of soil compaction to limit pipe deflections and stress.
Estimating Modulus of Soil Reaction
All of the evaluation starts from the basic idea that modulus of soil reaction, E’, is known a priori by the designer. Reality is quite different since E’ is often selected among available literature tables (Table 2).
To understand the influence of E’ on pipe deflections, the IOWA formula has been rewritten in terms of stiffness ratio, Rs (Equation [1-1]), assuming:
W = (γH)D = (E’εD), where ε is the soil strain and E’ is soil stiffness modulus
r3 = (D/2)3 = D3/8
K = 0.1
Dl = 1
d = (Δ/D) = pipe deflection

Equation [1-4] represents the IOWA formula as a relation between two dimensionless variables: d/εx = pipe deflection term; Rs = stiffness ratio term.
It can be noted (Figure 4) that such an equation approaches a horizontal asymptote at d/ε greater than 1 for high values of Rs and:
For Rs > 200, the pipe deflection term d/ε > 1, which implies that pipe deflection is greater than vertical sidefill compression (flexible pipes);
For Rs < 200, the pipe deflection term d/ε < 1, which implies that pipe deflection is less than vertical sidefill compression (rigid pipes).
Reynold K. Watkins & Albert B. Smith said empirical pipe deflections do not exceed vertical compression of the sidefill soil and maximum d/ε should be 1. Therefore, they proposed a formula (USU empirical) that does not exceed unity:
Conclusion
Experience has shown that pipe deflections are limited for standard pipeline burial depths; however, under some circumstances, excessive deflections have been measured even at shallow depths, causing delays during construction. Starting from the modified IOWA formula, the following conclusions can warn the designers in terms of pipe flexibility D/t:

Pipes with D/t < 50 can be considered rigid since they are stiffer than the backfill material surrounding it, do not present excessive ovalization, and are not influenced by sidefill stiffness. A proper bedding is important since they transmit most of the load through the pipe wall into the bedding.
Pipes with D/t Î [50; 100] can be normally considered flexible, offering significant structural benefits to the project. That is because if properly installed, they can be buried much deeper than a similarly installed rigid pipe because of the soil-pipe interaction, and will have a maximum deformation similar to the sidefill compression. Therefore, the control of deflection is obtained through the control of soil deformation by verifying backfill compaction level.
Pipes can experience high deflections and wall-bending stress even at shallow depth if a proper soil backfilling compaction is not done. Soil stiffness E’ value (in kPa) and modulus of soil reaction can be roughly estimated through the relation 1,000H (where H is the cover depth in meters) to limit pipe deflections to 3%












Comments